Least Squares

Model

System of equations:
$A\vec{x}=\vec{b}$
Where $A$ is $m\times n$, $x$ is $n\times 1$ and $b$ is $m\times 1$.
$A$ and $b$ are given (known), $x$ is unknown.

This may not have an explicit solution if:

• Overdetermined: $m>n$
  • More equations than unknowns
  • If the extra equations are inconsistent with the others, $b$ may fall outside $Col(A)$.
  • Ex. $Col(A)$ forms a plane in ${\mathbb{R}}^n$ but $b\in {\mathbb{R}}^m$
• Underdetermined: $m<n$
  • Fewer equations than unknowns
  • Even though there might be infinitely many solutions if $b\in Col(A)$, if $b$ isn’t in the span of the few available columns, no solution exists

Objective

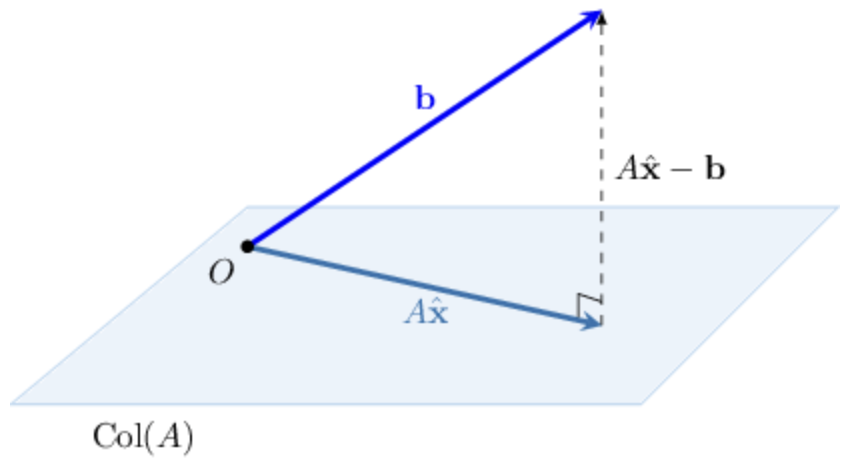
In this case, we want to find the vector $\hat{x}$ that minimizes the distance between $A\hat{x}$ and $b$.

$$\underset{\hat{x}}{\min }\Vert A\hat{x}-b{\Vert }_2$$

Visualization

Such a vector $A\hat{x}$ is the orthogonal projection of $b$ onto the subspace spanned by $Col(A)$.
This is from the definition of orthogonal projection.
An interesting connection with the visual is the Pythagorean theorem and triangle inequality.

Solution 1

We observe from above:
$(A\hat{x}-b)\perp Col(A)$
This is saying that $A\hat{x}-b$ is orthogonal to each column $a_i$ of $A$.
Thus, the dot product of the columns of $A$ and the vector $A\hat{x}-b$ must be 0:
$A^T(A\hat{x}-b)=0$
Expanding
$A^{T}A\hat{x}-A^{T}b=0$
$A^{T}A\hat{x}=A^{T}b$

Solution 2

Calculus approach to min the objective. TODO.

Normal Equation

$A^{T}A\hat{x}=A^{T}b$