Linear Algebra

Vectors and Lines

Vectors have magnitude and direction in ${\mathbb{R}}^n$ ($n$-tuple)
Line in ${\mathbb{R}}^n$ can be represented as

$$L=\{\vec{u}+\alpha \vec{v}|\alpha \in \mathbb{R}\}$$

Linear Combination

$$\sum _{i=0}^n{c}_i{\vec{v}}_i$$

$span$ of a set of vectors is the set of all possible linear combination of those vectors

• If the vector is 0, span is a point of that vector
• span of 1 vector is a line
• span of 2 vectors, where one is a lin comb of the other, is still a line
  • Called linearly dependent
• $span({\vec{v}}_1,{\vec{v}}_2)={\mathbb{R}}^2$ if linear combination of ${\vec{v}}_1,{\vec{v}}_2$ ‘covers’ ${\mathbb{R}}^2$
• $span$ of $n+1$ will guarantee that 1 of them is redundant (lin comb of some others)

Linear Dependence

A set of vectors is linearly dependent iff there is a linear combination that results in $\vec{0}$ with one of the constants being non-zero: $c_1{\vec{v}}_1+...c_n{\vec{v}}_n=\vec{0}$
Else, linearly independent.

Do systems of equation on example case to determine if it’s possible to write any vector $(a,b,c)$ as a lin combination of your vector set. Once you have an equation, see what the $c_i$ factors need to be to create a $\vec{0}$ , if they are all $0$, then lin independent.

Subspace

The set of vectors $V$ is a subset of ${\mathbb{R}}^n$
It is a subspace of ${\mathbb{R}}^n$ if:

1. Contains $\vec{0}$
2. $\forall c\in \mathbb{R},\forall x\in V;c\vec{x}\in V$ (closure under multiplication)
3. $\forall \vec{a}\in V,\forall \vec{b}\in V;\vec{a}+\vec{b}\in V$ (closure under addition)

Note: span of set $V$ (lin comb) is a subspace

BASIS

If $V$ is a subspace , its basis is a minimal set $S$ that spans $V$.
Minimal meaning linearly independent.

• Any set that spans $V$ must have at least size of $S$
  • Proof: If you have some set $V^{\prime }$ that spans $S$ and has less members than $V$, you can replace members of $V^{\prime }$ 1-by-1 with $V$ because members of $V$ will be able to be re-written as lin combinations of $V^{\prime }$ and you end up with a contradiction.
• $Dim(V)=$ size of any basis
• ex. If vectors are in ${\mathbb{R}}^n$ but basis size is 2, the subspace only spans ${\mathbb{R}}^2$
• Vector in some basis $\mathcal{B}$ : $[\vec{x}{]}_{\mathcal{B}}=[5;-2]=5{\vec{b}}_1-2{\vec{b}}_2$
• TODO: change of basis (inverse)

Vector Length and Product

$\vec{a}\cdot \vec{b}=a_1{b}_1+...+a_n{b}_n$ (scalar)
$\Vert \vec{a}{\Vert }^2=\vec{a}\cdot \vec{a}$
$|\vec{x}\cdot \vec{y}|\le \Vert \vec{x}\Vert \Vert \vec{y}\Vert$ (Cauchy Shwarz inequality)

• $\Vert \vec{x}+\vec{y}{\Vert }^2\le (\Vert \vec{x}\Vert +\Vert \vec{y}\Vert {)}^2$
• Remove the squares
• Triangle Inequality
• Geo intuition: vector formed by traveling from first to second will have length less than or equal to individual lengths’ sum (equal if vec is same)

$\Vert \vec{a}-\vec{b}{\Vert }^2=\Vert \vec{a}{\Vert }^2+\Vert \vec{b}{\Vert }^2-2\Vert \vec{a}\Vert \Vert \vec{b}\Vert cos\theta$ (Law of Cosines, triangle geo in n-dim)

• Expand using dot product definition on lhs
• $\vec{a}\cdot \vec{b}=\Vert \vec{a}\Vert \Vert \vec{b}\Vert cos\theta$
• So, if $\vec{a}\cdot \vec{b}=0$ , then $a,b$ are orthogonal!

$\frac{\vec{a}}{\Vert \vec{a}\Vert }=\vec{u}$ ; normalized unit vector

Planes

In ${\mathbb{R}}^3$, if you have a point on the plane ${\vec{p}}_1$ and take any other point on that plane $\vec{p}$, then a vector on that plane will be $\vec{p}-{\vec{p}}_1$. A normal vector $\vec{n}$ to that plane will mean that $\vec{n}\cdot (\vec{p}-{\vec{p}}_1)=0$ .

This means that $\vec{n}\cdot \vec{p}=\vec{n}\cdot {\vec{p}}_1$

Then, for a fixed/known ${\vec{p}}_1,\vec{n}$ you will get an equation that looks like $Ax+By+Cz=D$
Where $x,y,z$ are coordinates of $\vec{p}$ and $A,B,C$ are coordinates of $\vec{n}$.

Something something about calculating point distance to plane
Something something about calculating distance between two planes

Matrices

Basic definition

$$A=\left[\begin{array}{cc}a& b\\ c& d\end{array}\right],\vec{x}=\left[\begin{array}{c}x\\ y\end{array}\right]$$ $$A\vec{x}=\left[\begin{array}{c}ax+by\\ cx+dy\end{array}\right]$$

Row view:

$$A=\left[\begin{array}{c}{a}^T\\ b^T\end{array}\right]⟹A\vec{x}=\left[\begin{array}{c}{a}^T\cdot \vec{x}\\ b^T\cdot \vec{x}\end{array}\right]$$

Column view:

$$A=\left[\begin{array}{cc}\vec{a}& \vec{b}\end{array}\right]⟹A\vec{x}=x_1\vec{a}+x_2\vec{b}$$

This is now a linear combination of the column vectors of $A$.

Null space

$$N(A)=\{\vec{x}\in {\mathbb{R}}^n|A\vec{x}=\vec{0}\}$$

• The set of vectors that satisfy this is a subspace (refer to properties of subspace)
• Given an $A$, find rrech form, write $\vec{x}$ as a linear combination with free variables, can be written as $span({\vec{v}}_1,...)$

Connection with linear independence
$N(A)$ is the set of all $\vec{x}$ s.t.

$$A\vec{x}=x_1{\vec{v}}_1+...x_n{\vec{v}}_n=0$$

where ${\vec{v}}_i$ are column vectors of $A$.
Then from the definition, ${\vec{v}}_i$ are linearly independent if the only solution to the above is $\vec{x}=\vec{0}$

$Nullity(A)=Dim(N(A))=numfreevariablesofrref(A)$

Column space

$$A=\left[\begin{array}{ccc}{\vec{v}}_1& ...& {\vec{v}}_n\end{array}\right];C(A)=span({\vec{v}}_1,...,{\vec{v}}_n)=\{A\vec{x}|\vec{x}\in {\mathbb{R}}^n\}$$

• Like null space, this is also a subspace
• Reminder about $span$ being all possible linear combinations of the vectors
• If $N(A)=\{\vec{0}\}$ this means the cols are linearly independent, so they form a basis for $C(A)$.
  • Dependent ones will be the free variables of $\vec{x}$ after rref
  • You can show that you can write those columns of $A$ as lin. comb. of the others by setting the remaining free variables to $0$
    • therefore they are redundant and the basis is the remaining columns
• Something something about plane equation from the basis
• $Rank(A)=Dim(C(A))$ i.e. find the size of the basis of $C(A$) (number of pivot cols of rref)

Properties of matrices

$A+B=B+A;(commutativity)$
$A+(B+C)=(A+B)+C;(associativity)$
$A+0=A$ ; where 0 is a matrix of zeros
$A+(-A)=0$ ;
$A(BC)=(AB)C;(associativity)$
$A(B+C)=AB+AC;distributivelaw$
$(A+B)C=AC+BC;distributivelaw$

In general $AB\ne BA$
It could be that $AB=0$ even if $A\ne 0$ and $B\ne 0$
so, some things are not like scalars

Diagonal Matrix

$$\left[\begin{array}{cc}a& 0\\ 0& b\end{array}\right]$$

Identity Matrix

$$I=\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]$$

Matrix Decomposition

Let $E_{ij}=$ matrix with a 1 in position $i,j$ and 0’s elsewhere. Then we have

$$A=\left[\begin{array}{cc}a& b\\ c& d\end{array}\right]=a{E}_{11}+b{E}_{12}+c{E}_{21}+d{E}_{22}$$

Then, we can write matrix multiplication as:

$$AB=(a{E}_{11}+b{E}_{12}+c{E}_{21}+d{E}_{22})(e{E}_{11}+f{E}_{12}+g{E}_{21}+h{E}_{22})$$

Inverse

An inverse matrix $A^{-1}$ is one where the following holds:

$$A{A}^{-1}=I$$

How to find it? Use adjoint of $A$ called $A^{\ast }$ :

$$A^{\ast }=\left[\begin{array}{cc}d& -b\\ -c& a\end{array}\right]$$

Then:

$$A{A}^{\ast }=\left[\begin{array}{cc}a& b\\ c& d\end{array}\right]\left[\begin{array}{cc}d& -b\\ -c& a\end{array}\right]=\left[\begin{array}{cc}ad-bc& 0\\ 0& ad-bc\end{array}\right]=(ad-bc)\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]=det(A)I$$

Define $det(A)=(ad-bc)$.

Now, if $det(A)\ne 0$ , then we can find that

$$A^{-1}=\frac{1}{det(A)}{A}^{\ast }$$

Some findings
$(AB{)}^{-1}=B^{-1}{A}^{-1}$
$det(AB)=det(A)det(B)$

1-1 functions and Null Space

A function that is 1:1 means it’s inverse is also a function (functions may map many-one, meaning inverse is not a function).

Reminder on Null Space

$$N(A)=\{\vec{x}\in {\mathbb{R}}^n|A\vec{x}=\vec{0}\}$$

If $N(A)$ has a non-trivial solution, then $A$ is a many-one function.
Proof: for any ${\vec{x}}_1\in N(A)$ , we can add this to any $Ax=b$ solution.

Linear Transformations/Functions

A transformation $T:R^n\to R^m$ is linear if it satisfies

$$T(\vec{u}+\vec{v})=T(\vec{u})+T(\vec{b})$$ $$T(\alpha \vec{u})=\alpha T(\vec{u})$$

or all in one

$$T(\alpha u+\beta v)=\alpha T(u)+\beta T(v)$$

We can show that $Ax$ is a linear transformation: $T(x)$:

$$A(\vec{u}+\vec{v})=A\vec{u}+A\vec{v};A(\alpha \vec{v})=\alpha A\vec{v}$$

(distributive rule)

Matrices are Linear Transformations

$$T(\vec{x})=A\vec{x}$$

Given that $A$ is $m$ rows by $n$ columns

$$T:{\mathbb{R}}^n\to {\mathbb{R}}^m$$

AND it is a linear transformation.

Function composition is Matrix Multiplication

Exploring Matrices as Linear Transformations

Dilations: Diagonal matrices (stretch initial vector)
Rotations: TODO

• From 3blue1brown:
  • Matrix cols are what happened to the basis vectors (ihat jhat)
  • Doing the same thing that happened to the basis vectors onto some new vector

$$T(\vec{x})=T(x_1{\vec{e}}_1+...)=x_{1}T({\vec{e}}_1)+...=T\vec{x}$$

Where at the end, $T$ is a matrix where the columns are the basis vectors with the transformation applied to them. At the beginning, $T()$ is any linear transformation.

Projection Onto Line

$$Pro{j}_L(\vec{x})=(\frac{\vec{x}\cdot \vec{v}}{\vec{v}\cdot \vec{v}})\vec{v}=(\vec{x}\cdot \hat{u})\hat{u}$$

Pick any $\vec{x}$ , and project onto a line that is drawn by $c\vec{v}$ .

Projection formula origin. Note that $k\vec{a}$ is what we want to find.

$\vec{x}=k\vec{a}+\vec{z};k\in \mathbb{R},z\perp a$
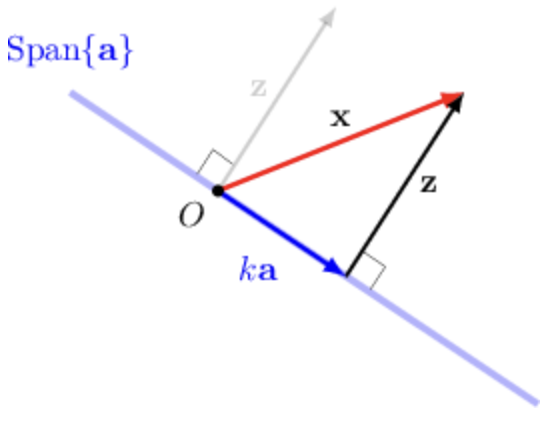
Multiply by $\vec{a}$ both sides, and due to $z\perp a$ we get:
$\vec{x}\cdot \vec{a}=k(\vec{a}\cdot \vec{a})$

Therefore our goal, projection of $\vec{x}$ onto $span(a)$ is:
$Pro{j}_a(\vec{x})=k\vec{a}=\frac{(\vec{x}\cdot \vec{a})}{\vec{a}\cdot \vec{a}}\vec{a}$

If $\{{\vec{a}}_1,{\vec{a}}_2,\dots ,{\vec{a}}_n\}$ is a set of orthogonal vectors, then the orthogonal projection of a vector $\vec{x}$ onto the subspace $S=\text{Span}\{{\vec{a}}_1,{\vec{a}}_2,\dots ,{\vec{a}}_n\}$ is given by

$${\text{proj}}_S\vec{x}={\text{proj}}_{{\vec{a}}_1}\vec{x}+{\text{proj}}_{{\vec{a}}_2}\vec{x}+\cdots +{\text{proj}}_{{\vec{a}}_n}\vec{x}$$ $$=\frac{\vec{x}\cdot {\vec{a}}_1}{{\vec{a}}_1\cdot {\vec{a}}_1}{\vec{a}}_1+\frac{\vec{x}\cdot {\vec{a}}_2}{{\vec{a}}_2\cdot {\vec{a}}_2}{\vec{a}}_2+\cdots +\frac{\vec{x}\cdot {\vec{a}}_n}{{\vec{a}}_n\cdot {\vec{a}}_n}{\vec{a}}_n.$$

In other words, the orthogonal projection of $\vec{x}$ onto $S=\text{Span}\{{\vec{a}}_1,{\vec{a}}_2,\dots ,{\vec{a}}_n\}$ is the sum of the orthogonal projections of $\vec{x}$ onto each one-dimensional subspace of $\text{Span}\{{\vec{a}}_1,{\vec{a}}_2,\dots ,{\vec{a}}_n\}$.

Watch out! The formula works only when the set of vectors $\{{\vec{a}}_1,{\vec{a}}_2,\dots ,{\vec{a}}_n\}$ is orthogonal!

In the case of a 2-dimensional subspace $S=\text{Span}\{{\vec{a}}_1,{\vec{a}}_2\}$, we can visualize the orthogonal projection geometrically, as follows:

$${\text{proj}}_S\vec{x}={\text{proj}}_{{\vec{a}}_1}\vec{x}+{\text{proj}}_{{\vec{a}}_2}\vec{x}$$

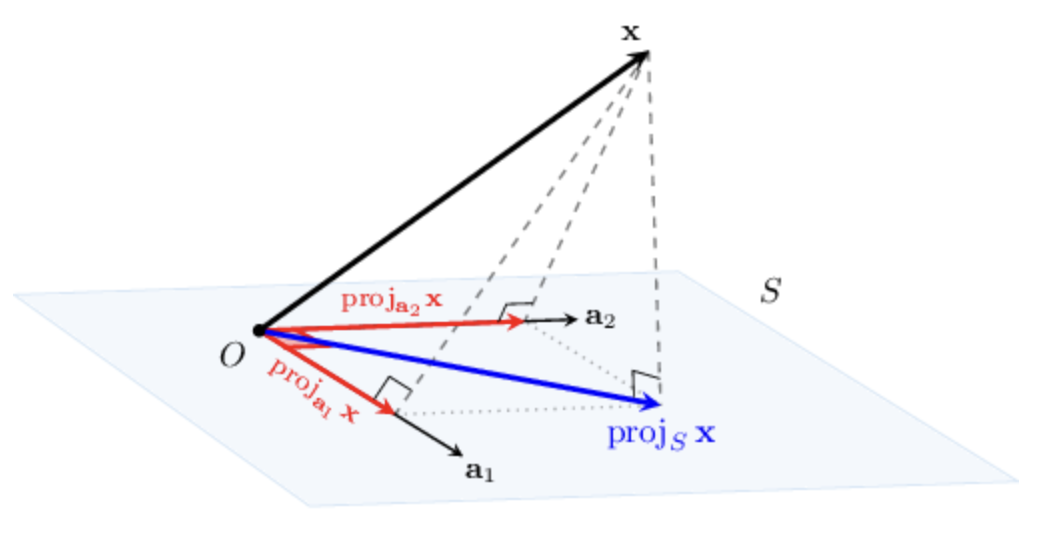
Projection Onto Any Subspace

GOAL: Find the orthogonal projection ${\vec{x}}_S$ of the vector $\vec{x}$ onto the subspace $S=\text{Span}\{{\vec{a}}_1,{\vec{a}}_2\}$

• Notice that since ${\vec{a}}_1\cdot {\vec{a}}_2\ne 0$, the vectors ${\vec{a}}_1$ and ${\vec{a}}_2$ are not orthogonal.

Write $\vec{x}$ as

$$\vec{x}={\vec{x}}_S+{\vec{x}}_{S^{\perp }},$$

where ${\vec{x}}_S=k_1{\vec{a}}_1+k_2{\vec{a}}_2\in S$ and ${\vec{x}}_{S^{\perp }}\in S^{\perp }$.

---

Step 1: Projection Relation

$${\vec{x}}_{S^{\perp }}=\vec{x}-{\vec{x}}_S=\vec{x}-(k_1{\vec{a}}_1+k_2{\vec{a}}_2)=\vec{x}-k_1{\vec{a}}_1-k_2{\vec{a}}_2.$$

Since ${\vec{x}}_{S^{\perp }}\in S^{\perp }$, that is, ${\vec{x}}_{S^{\perp }}\perp S$,

$$\{\begin{array}{l}{\vec{x}}_{S^{\perp }}\cdot {\vec{a}}_1=0\\ {\vec{x}}_{S^{\perp }}\cdot {\vec{a}}_2=0\end{array}⟹\{\begin{array}{l}(\vec{x}-k_1{\vec{a}}_1-k_2{\vec{a}}_2)\cdot {\vec{a}}_1=0\\ (\vec{x}-k_1{\vec{a}}_1-k_2{\vec{a}}_2)\cdot {\vec{a}}_2=0.\end{array}$$

---

Step 2: System of Equations

Now, we substitute the expression for ${\vec{x}}_{S^{\perp }}$ into the system to get

$$\{\begin{array}{l}{k}_1({\vec{a}}_1\cdot {\vec{a}}_1)+k_2({\vec{a}}_2\cdot {\vec{a}}_1)=(\vec{x}\cdot {\vec{a}}_1)\\ k_1({\vec{a}}_1\cdot {\vec{a}}_2)+k_2({\vec{a}}_2\cdot {\vec{a}}_2)=(\vec{x}\cdot {\vec{a}}_2).\end{array}$$

We can write this system in an equivalent matrix form as follows:

$$\left[\begin{array}{cc}{\vec{a}}_1\cdot {\vec{a}}_1& {\vec{a}}_2\cdot {\vec{a}}_1\\ {\vec{a}}_1\cdot {\vec{a}}_2& {\vec{a}}_2\cdot {\vec{a}}_2\end{array}\right]\left[\begin{array}{c}{k}_1\\ k_2\end{array}\right]=\left[\begin{array}{c}\vec{x}\cdot {\vec{a}}_1\\ \vec{x}\cdot {\vec{a}}_2\end{array}\right].$$

---

Step 3: Matrix Representation

Denote

$$A=\left[\begin{array}{cc}{\vec{a}}_1& {\vec{a}}_2\end{array}\right]\text{and}\vec{k}=\left[\begin{array}{c}{k}_1\\ k_2\end{array}\right],$$

then

$$A^{T}A\vec{k}=A^T\vec{x}⟹\vec{k}=(A^{T}A{)}^{-1}{A}^T\vec{x}.$$

Therefore,

$${\text{proj}}_S\vec{x}=A\vec{k}=A(A^{T}A{)}^{-1}{A}^T\vec{x}.$$

This is a formula for the orthogonal projection!

---

Comparison with line projection

The orthogonal projection of a vector $\vec{x}$ onto the one-dimensional subspace $\text{Span}\{\vec{a}\}$ is given by

$${\text{proj}}_{\vec{a}}\vec{x}=\frac{\vec{a}\cdot \vec{x}}{\vec{a}\cdot \vec{a}}\vec{a}.$$

we can re-write it like:

$${\text{proj}}_{\vec{a}}\vec{x}=\left[\frac{a^T\vec{x}}{a^{T}a}\right]\vec{a}$$ $$=\left[(a^{T}a{)}^{-1}{a}^T\vec{x}\right]\vec{a}$$ $$=\vec{a}(a^{T}a{)}^{-1}{a}^T\vec{x}.$$

Linear and Bilinear Forms

Linear form: $f(\vec{x})={\vec{a}}^T\vec{x}$ where $\vec{a}\in {\mathbb{R}}^n$ .
Bilinear form:
Suppose $A$ is an $n\times n$ matrix. Then, the function $B:{\mathbb{R}}^n\times {\mathbb{R}}^n\to \mathbb{R}$ defined as

$$B(\mathbf{x},\mathbf{y})={\mathbf{x}}^{T}A\mathbf{y},\mathbf{x},\mathbf{y}\in {\mathbb{R}}^n,$$

is linear in each argument separately. That’s the reason why we call them bilinear.

• For $\mathbf{y}$ fixed, all $\mathbf{u},\mathbf{v}\in {\mathbb{R}}^n$, and any real constant $c$, linearity in the first argument means the following:

$$B(\mathbf{u}+\mathbf{v},\mathbf{y})=B(\mathbf{u},\mathbf{y})+B(\mathbf{v},\mathbf{y})$$ $$B(c\mathbf{u},\mathbf{y})=cB(\mathbf{u},\mathbf{y})$$

• For $\mathbf{x}$ fixed, all $\mathbf{w},\mathbf{z}\in {\mathbb{R}}^n$, and any real constant $c$, linearity in the second argument means the following:

$$B(\mathbf{x},\mathbf{w}+\mathbf{z})=B(\mathbf{x},\mathbf{w})+B(\mathbf{x},\mathbf{z})$$ $$B(\mathbf{x},c\mathbf{w})=cB(\mathbf{x},\mathbf{w})$$

Eigen-everything

Eigenvectors: “natural” directions of the matrix/linear transformation that represent only a scaling/stretch.
$A\vec{v}=\lambda \vec{v}$

Diagonalize

A square matrix $A$ is called diagonalizable if there exists a diagonal matrix $D$ and an invertible matrix $P$ such that:

$$A=PD{P}^{-1}.$$

If $A$ is a $2\times 2$ matrix, then it is diagonalizable if and only if there exists a basis of ${\mathbb{R}}^2$ that consists of eigenvectors of $A$.

We can break this down into two possible cases:

• Case 1: If $A$ has two distinct eigenvalues, then it is indeed diagonalizable. This is because two distinct eigenvalues will give rise to two linearly independent eigenvectors (one for each eigenvalue).

  So, for a matrix $A$ with eigenvalues ${\lambda }_1$ and ${\lambda }_2$ and corresponding eigenvectors ${\vec{v}}_1$ and ${\vec{v}}_2$, we have

  $$A=\underset{P}{\underbrace{\left[\begin{array}{cc}{\vec{v}}_1& {\vec{v}}_2\end{array}\right]}}\underset{D}{\underbrace{\left[\begin{array}{cc}{\lambda }_1& 0\\ 0& {\lambda }_2\end{array}\right]}}\underset{P^{-1}}{\underbrace{{\left[\begin{array}{cc}{\vec{v}}_1& {\vec{v}}_2\end{array}\right]}^{-1}}}.$$

• Case 2: If we get a double root $\lambda$ of the characteristic equation, the matrix will be diagonalizable only if we can find exactly two linearly independent eigenvectors corresponding to $\lambda$, which may or may not be possible. Another way of saying this is that the corresponding eigenspace $V_{\lambda }$ must be of dimension 2.

Geometrical Interpretation:

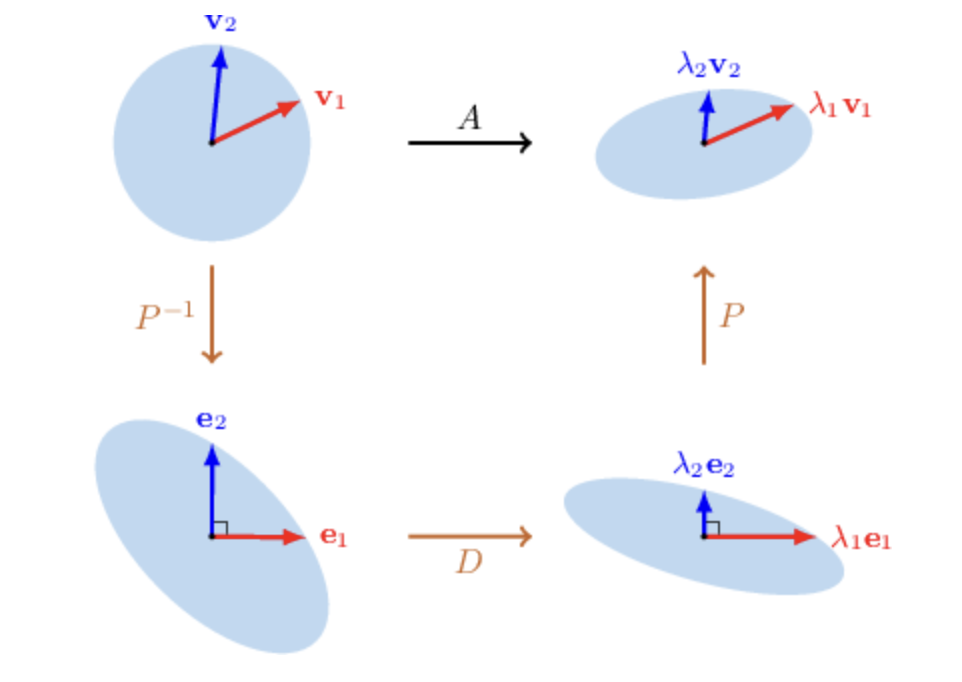
• The matrix $P^{-1}$ changes the coordinates of any vector of the plane from the standard basis $\{{\vec{e}}_1,{\vec{e}}_2\}$ to the basis of eigenvectors $\{{\vec{v}}_1,{\vec{v}}_2\}$.

• The diagonal matrix $D$ scales the 1st and 2nd coordinates by ${\lambda }_1$ and ${\lambda }_2$, respectively.

• Finally, the matrix $P$ changes the coordinates of the result back to the standard basis.

Matrix Powers

From diagonalization we have:
$A=PD{P}^{-1}$
$A^2=PD{P}^{-1}PD{P}^{-1}=P{D}^2{P}^{-1}$
This generalizes to:
$A^n=P{D}^n{P}^{-1}$