e

$$\underset{n\to \infty }{\lim }(1+\frac{1}{n}{)}^n=e\approx 2.71828$$

Compound interest where you make the compounding rate infinitesimally small.

$$e=1+\frac{1}{1!}+\frac{1}{2!}+\frac{1}{3!}\dots$$

Formal Derivation

This is one approach to arrive at $e$ from $ln$

ln Definition

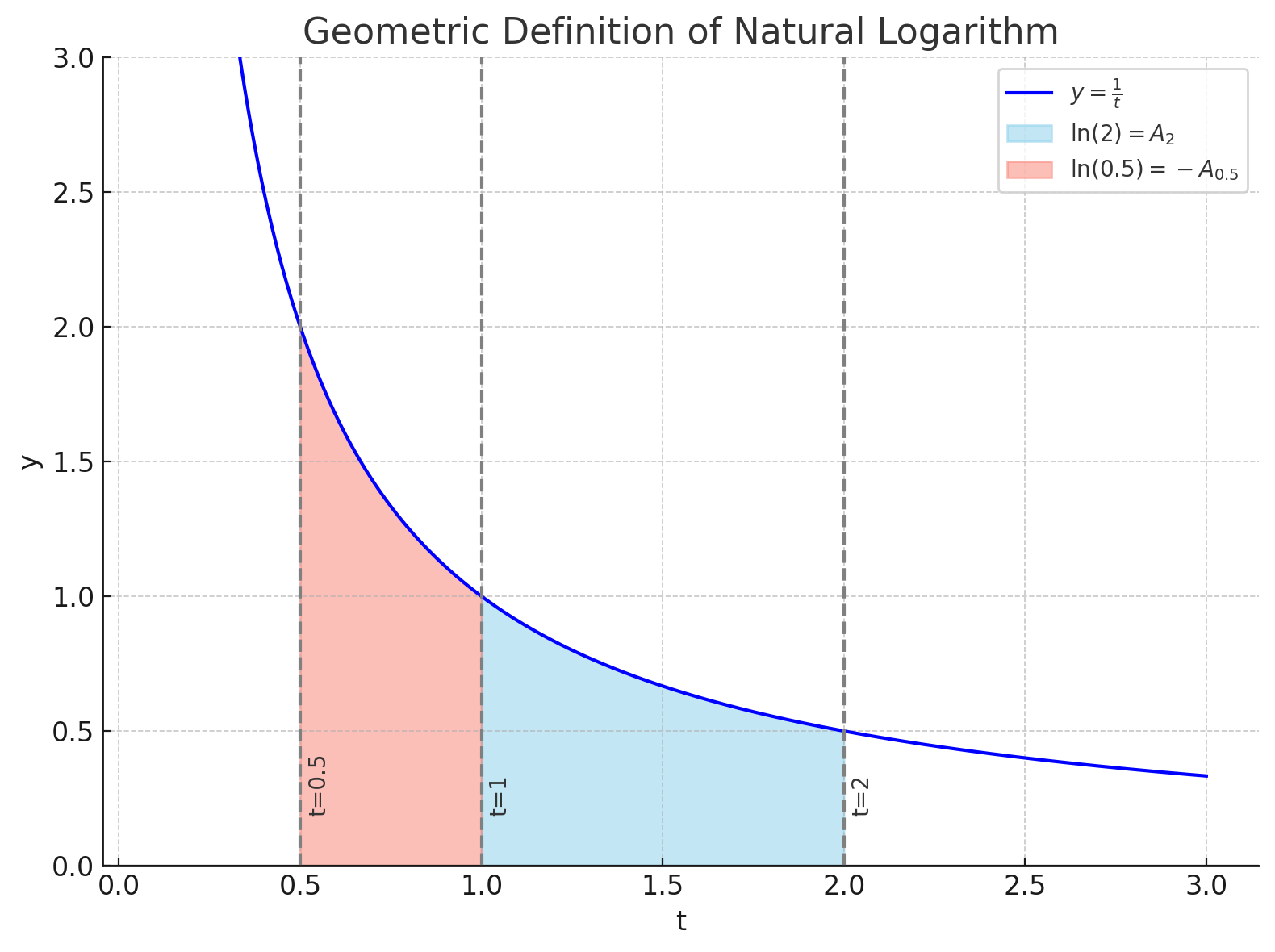
For $x>0$ , let $A_x$ be the area of the region in the $yt$-plane bounded by the curve $y=1/t$ , the $t$-axis, and the vertical lines $t=1$ and $t=x$.
Define:

$$ln(x)=\{\begin{array}{ll}{A}_x& x\ge 1\\ -A_x& 0<x<1\end{array}$$

Note that the domain of $ln$ is $(0,\infty )$, $f(x)>0$ for $x>1$, $f(x)<0$ for $0<x<1$, and $f(1)=0$.

Note that these properties all hold for $f(x)={\log }_a(x)$ when $a>1$.

---

Theorem 1: Derivative of ln

Let $f(x)=\ln (x)$. Then

$$f^{\prime }(x)=\frac{1}{x}$$

Note: this is a special case of the Fundamental Theorem of Calculus.

Proof

Let $x>0$. Apply the definition:

$$\frac{d}{dx}\ln (x)=\underset{h\to 0}{\lim }\frac{\ln (x+h)-\ln (x)}{h}$$

For $ln(x+h)-ln(x)$, from the graph, we see that for $h>0$, the small rectangle is (width x height)

$$h\cdot \frac{1}{x+h}$$

and the large rectangle is at the earlier point

$$h\cdot \frac{1}{x}$$

thus,

$$\frac{h}{x+h}<\ln (x+h)-\ln (x)<\frac{h}{x};$$

this is clear if $x>1$, but in fact it is true for all $x$. Thus,

$$\frac{1}{x+h}<\frac{\ln (x+h)-\ln (x)}{h}<\frac{1}{x}$$

By the squeeze theorem

$$f^{\prime }(x)=\frac{1}{x}$$

Note: same argument works for $h<0$

Theorem 2: Properties of ln(x)

1. $\ln (xy)=\ln (x)+\ln (y)$
2. $\ln (1/x)=-\ln (x)$
3. $\ln (x/y)=\ln (x)-\ln (y)$
4. $\ln (x^r)=r\ln (x)$

Proof

(i) Fix $y>0$, and let $g(y)=\ln (xy)-\ln (x)$.
By chain rule,

$$g^{\prime }(y)=\frac{y}{xy}-\frac{1}{x}=0$$

So, $g(y)$ is constant as a function of $x$.
For $x=1$ , $g(y)=\ln (y)-\ln (1)=\ln (y)$ , but if $g$ is constant then $\forall x$

$$\ln (xy)-\ln (x)=\ln (y)$$

therefore

$$\ln (xy)=\ln (x)+\ln (y)$$

(ii) $0=\ln (1)=\ln (\frac{x}{x})=\ln (x)+\ln (\frac{1}{x})$ last part is due to (i)
re-arranging we get

$$\ln (1/x)=-\ln (x)$$

(iii) $\ln (x/y)=\ln (x)+\ln (1/y)=\ln (x)-\ln (y)$

(iv) for integers, expand $x^r$ into either $(x\cdot x\dots )$ or $(1/x\cdot 1/x\dots )$ then apply (i) and (ii) recursively to get:

$$\ln (x^r)=r\ln (x)$$

for rational $m/n$ start with:

$$n\ln (x^{m/n})=\ln (x^m)=m\ln (x)$$

therefore

$$ln(x^{m/n})=(m/n)ln(x)$$

Exponential Function

Since $\ln (x)$ is 1:1, it has an inverse function called the exponential function:
$exp(y)$ is the unique $x$ s.t. $y=ln(x)$.

$$x=exp(y)⟺y=ln(x)$$

Normally we end up reversing roles and $y=exp(x)$.

Theorem 3: properties of exp

$exp(0)=1$ is a given from $ln(1)=0$.

1. $exp(x+y)=exp(x)exp(y)$
2. $exp(-x)=1/exp(x)$
3. $exp(x-y)=exp(x)/exp(y)$
4. $(exp(x){)}^r=exp(rx)$

Proof

(i)

$$\ln (\exp (x+y))=x+y=\ln (\exp (x))+\ln (\exp (y))=\ln (\exp (x)\exp (y))$$

Since ln is 1:1, $\exp (x+y)=\exp (x)\exp (y)$
(ii)

$$1=exp(0)=exp(x-x)=exp(x)exp(-x)⟹exp(-x)-1/exp(x)$$

(iii) from (i) and (ii).
(iv) from recursive (i).

Derivative of exp

Inverse function theorem (diff & chain rule on $x=f(f^{-}1(x))$):

$$(f^{-}1{)}^{\prime }(x)=\frac{1}{f^{\prime }(f^{-}1(x))}$$

For $f=ln$ and $f^{-}1=exp$:

$$\frac{d}{dx}exp(x)=1/l{n}^{\prime }(exp(x))=1/(1/exp(x))=exp(x)$$

WOW.

e

Define $e=\exp (1)$.
Using (iv):

$$e^r=(exp(1){)}^r=exp(r\cdot 1)=exp(r)$$

So, $\forall x\in \mathbb{R}$ define

$$e^x=\exp (x)$$

a^x

$$a^x=(e^{ln(a)}{)}^x=e^{xln(a)}$$

Taking derivative of RHS using chain rule we get:

$$\frac{d}{dx}{a}^x=ln(a)a^x$$

log

Defn: for $a>0,a\ne 1,lo{g}_a(x)$ is defined to be the inverse of $a^x$ s.t.

$$a^{lo{g}_a(x)}=x$$

$⟹x=e^{lo{g}_a(x)ln(a)}$ from $a^x$ definition
$⟹ln(x)=lo{g}_a(x)ln(a)$
$⟹lo{g}_a(x)=\frac{ln(x)}{ln(a)}$

Compound Interest Definition

$$e^x=\underset{n\to \infty }{\lim }(1+\frac{x}{n}{)}^n$$

Proof

$$\underset{n\to \infty }{\lim }ln((1+\frac{x}{n}{)}^n)=\underset{n\to \infty }{\lim }nln(1+x/n)$$

Apply substitution $h=x/n\to 0$

$$=\underset{h\to 0}{\lim }\frac{x}{h}ln(1+h)=x\underset{h\to 0}{\lim }\frac{ln(1+h)-ln(1)}{h}=x$$

Last part is derivative of $ln(t)$ at $t=1$.

$$\underset{n\to \infty }{\lim }(1+x/n{)}^n=e^{ln({\lim }_{n\to \infty }(1+x/n{)}^n)}=e^x$$