2) Discrete Random Variables

2.1 Basic Concepts

• Random Variable (RV): A function that assigns a numerical value to each outcome of an experiment.
  • A random variable is called discrete if it can take a finite or countably infinite number of values.
  • Example: The number of heads in a sequence of coin tosses.

2.2 Probability Mass Function (PMF)

• The Probability Mass Function (PMF) of a discrete random variable $X$ is denoted by $p_X(x)$ and represents the probability that $X=x$: $$p_X(x)=P(X=x)$$
  • For all $x$: $$\sum _x{p}_X(x)=1$$
• Example: If $X$ represents the number of heads in two independent tosses of a fair coin, the PMF of $X$ is: $$p_X(x)=\{\begin{array}{ll}\frac{1}{4}& \text{if }x=0\text{ or }x=2\\ \frac{1}{2}& \text{if }x=1\\ 0& \text{otherwise}\end{array}$$

2.3 Functions of Random Variables

• A function $g(X)$ of a random variable $X$ is itself a random variable.
• The PMF of $g(X)$ can be computed from the PMF of $X$.

2.4 Expectation, Mean, and Variance

• Expectation or Mean: The expected value of a discrete random variable $X$ is: $$E[X]=\sum _{x}x{p}_X(x)$$
• Moment (n-th):
  $E[X^n]$
• Variance: The variance of $X$ measures the spread of its values:
  $Var(X)=E[(X-E[X]{)}^2]$
  $=E[X^2-2E[X]X+(E[X]{)}^2]$
  $=E[X^2]-2E[X]E[X]+(E[X]{)}^2$

$$\text{Var}(X)=E[X^2]-(E[X]{)}^2$$

• Standard Deviation: measures spread (like variance) but same units as $X$
  ${\sigma }_X=\sqrt{var(X)}$

Expected Value rule for Functions of Random Variables

$E[g(X)]={\sum }_{x}g(x)p_X(x)$

2.5 Joint PMFs of Multiple Random Variables

• Joint PMF: For two random variables $X$ and $Y$, the joint PMF is $p_{X,Y}(x,y)$, which gives the probability of the event $X=x$ and $Y=y$: $$p_{X,Y}(x,y)=P(X=x,Y=y)$$
  • The marginal PMF of $X$ is obtained by summing over all possible values of $Y$:
  $$p_X(x)=\sum _y{p}_{X,Y}(x,y)$$

Table example

2.6 Conditioning

• Conditional PMF: The conditional PMF of $X$ given $Y=y$ is: $$p_{X|Y}(x|y)=\frac{p_{X,Y}(x,y)}{p_Y(y)},\text{if }{p}_Y(y)>0$$

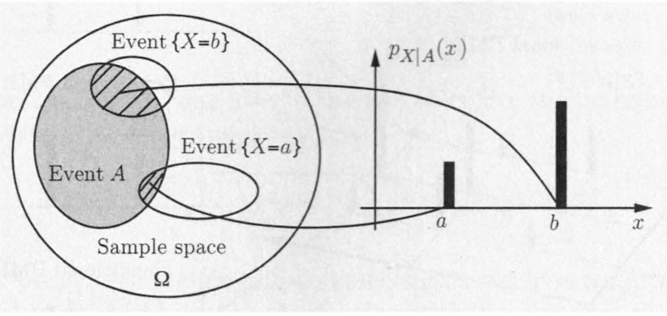
• The Total Expectation Theorem relates the expectation of $X$ to the conditional expectations:

$$E[X]=\sum _y{p}_Y(y)E[X|Y=y]$$

2.7 Independence

• Two random variables $X$ and $Y$ are independent if: $$p_{X,Y}(x,y)=p_X(x)p_Y(y)\text{for all }x,y$$

Special Discrete Random Variables

1. Bernoulli Random Variable:

   • A Bernoulli random variable takes two values, typically 0 and 1.
   • PMF: $$p_X(x)=\{\begin{array}{ll}p& \text{if }x=1\\ 1-p& \text{if }x=0\end{array}$$
   • Expectation: $E[X]=p$, Variance: $\text{Var}(X)=p(1-p)$

2. Binomial Random Variable:

   • A sum of independent Bernoulli trials.
   • PMF: $$p_X(k)=\left(\genfrac{}{}{0ex}{}{n}{k}\right)p^k(1-p{)}^{n-k},k=0,1,\dots ,n$$
   • Expectation: $E[X]=np$, Variance: $\text{Var}(X)=np(1-p)$
   • See 1.6 Independence for intuition

3. Geometric Random Variable:

   • Counts the number of trials until the first success.
   • PMF: $$p_X(k)=(1-p{)}^{k-1}p,k=1,2,\dots$$
   • Expectation: $E[X]=\frac{1}{p}$, Variance: $\text{Var}(X)=\frac{1-p}{p^2}$

4. Poisson Random Variable:

   • Approximation of Binomial where $p$ is small and $n$ is large.
   • PMF: $$p_X(k)=e^{-\lambda }\frac{{\lambda }^k}{k!},k=1,2,\dots$$
   • Expectation: $E[X]=\lambda$, $Var(X)=\lambda$
   • See 6) Bernoulli and Poisson